Омск, Омская область, Россия
Омск, Омская область, Россия
Данная статья посвящена гармонизации комплектов электронных заданий, предлагаемых для выполнения в классе и на расстоянии. Целью исследования является разработка универсального алгоритма для выбора «идеала», то есть наиболее комфортного комплекта, сбалансированного по цветовой гамме, количеству иллюстраций, пояснений и другим характеристикам. Методика предусматривает активное применение поисковых алгоритмов. В настоящее время для многих информационных дисциплин накоплено огромное количество примеров, в том числе онлайн, различных по сложности, оформлению, программной реализации и спектру приобретаемых умений и навыков. Проблема состоит в выборе наилучших из них, как и в объединении разнопланового электронного материала в наиболее комфортный и гармоничный по содержанию, характеристикам комплект. Метод позволяет учесть мнение студентов, реальное количество и скорость выполнения примеров на практике; оценить воздействие вероятных факторов (цвет, форма, справочная система, видео и звуковая подсказка и т.д.), влияющих на эргономику электронных заданий прямо или косвенно. В качестве теоретической платформы использованы аспекты методик и опыт массовых отборов из творческого наследия В.А. Савицкой.
образование, эргономика, комфорт, модель, регрессия, виртуальный выбор, идеал
Введение
Персональные компьютеры обеспечивают высокую скорость и комфортность решения учебных задач, поэтому перспективно объединять электронные примеры в комплекты, рассчитанные на выполнение в пределах одного занятия.
Комплекты, в свою очередь, совершенствуются: возникает некоторое абстрактное, эфемерное понятие «идеального» набора, в котором основополагающие по теме задания дополнены полезными тренажерами – для тренировки наблюдательности, логического мышления, расслабления глаз, восстановления сил.
Для многих дисциплин накоплено большое количество упражнений, в том числе и онлайн – различных по сложности, оформлению, программной реализации и спектру приобретаемых навыков и умений.
Тем не менее, подобрать удачный, т.е. «идеальный» набор заданий, пригодный и для обучения на расстоянии – по цветовой гамме, количеству иллюстраций, количеству интерактивных подсказок, не так нелегко.
Ощущение комфорта зависит от предпочтений, моды, ориентиров будущей профессии, участия в социальных сетях, статуса в электронном социуме – зачастую, нет точных границ, критериев, чтобы определить, насколько легким или сложным, подробным или лаконичным, цветным или монохромным должен быть пример.
Эргономика учитывает тонкие детали, слабо формализуемые, эфемерные составляющие, поэтому целесообразно обратиться к опыту тех сфер, где гармонизированные или «идеализированные» выборки, модели успешно применялись [1].
Предлагаемый алгоритм гармонизации комплекта электронных заданий позволит оптимизировать объем текста и количества иллюстраций в примерах, повысить комфортность работы.
- «Идеальный» выбор – как теоретическая концепция
Человек, его интеллектуальные возможности и техника находятся в непрерывном взаимовлиянии. Как маркетинговый прием, «виртуальный выбор» находит широкое применение при распространении программных продуктов и услуг. Однако в образовании электронные тренажеры и примеры ориентированы на приобретение полезных навыков и знаний, т.е. комфорт на занятиях – не самоцель.
В плане нейропсихологического воздействия на пользователя эргономичный фактор идентичен триггеру – некоему скрытому механизму, запускающему тот или иной элемент мотивации за счет улучшения условий – толчка к выбору правильного действия, принятия решения.
В целом, эргономические исследования базируются не только на расширении общих знаний о человеческих способностях и компетенциях и их влиянии на успешность деятельности пользователей, но и на исследованиях новых путей измерения профессионально-важных качеств, М.Ю. Рытов, В.В. Спасенников [7].
Мощное информационное давление на человека, по мнению Н.И. Барсуковой, оказывает системно организованная природная среда, принуждая адекватно воспринимать её гармоничные формы [2].
Эксплуатируя технику, человек совершенствует ее, улучшая эргономические показатели, так или иначе, старается достичь максимальной гармонии, стремиться к идеалам. Эти процессы находят свое отражение и при создании компьютерных примеров и тренажеров, и имеют психологическую составляющую.
По мнению С.Ф. Сергеева, феномены, имеющие ярко выраженную психологическую компоненту, включают эволюционные и аутопоэтические формы системных образований, их порождает интернет + системы мобильной коммуникации, развитие глобальной интеллектуальной социально-коммуникационной информационно-управляющей среды [9].
Современные электронные задания могут быть оформлены, озвучены так же гармонично, как и картины в музее, на художественной выставке, как музыкальные произведения.
Основа построения любой гармоничной среды, как указывает Н.И. Барсукова – понимание таких чувственно-полярных взаимоотношений, как свет и тень, жёсткое и мягкое, чёрное и белое, вертикаль и горизонталь и других контрастных сочетаний [9].
C учетом особенностей и психологии визуального восприятия пользователей общий дизайн, как полагает Е.В. Вехтер, должен способствовать вовлечению в информацию визуальных знаков и возможных вариант цветовых палитр [3].
Чувство цвета, формы, законченности и соразмерности композиционного расположения объектов, как отмечает Н.И. Барсукова, чувство «хорошей фигуры» и линии, чувство гармонии и дисгармонии, консонанса и диссонанса, чувство пропорции– весь этот огромный потенциал сенсорных возможностей организма является необходимым условием полноценной встречи личности с художественно организованной средой, проектируемой дизайнером [2].
Когнитивная эргономика [11],[12] рассматривается как систематическая основа для проектирования пользовательского интерфейса (T.P. Moran, 1981; G.C. Van der Veer, 2008).
С другой стороны, современный интерфейс и дизайн программных продуктов оказывает обратное влияние на развитие техники.
Как считает С.А. Багрецов [1], применение активной стратегии актуализации потенциальных свойств человеко-машинных комплексов, создание познавательных средств для более детального изучения субъект-объектных отношений в современной техносфере содействует раскрытию потенциальности создаваемых технических объектов.
Гармония компьютерных заданий складывается из многих составляющих и предполагает знание пропорций, умение рационально использовать пространство, применение знаковых средств, лаконичных наименований и кодировок, созвучных выполняемым действиям.
Педагогическая задача усложняется в том (Ю. Д. Овчинников, 2022), что давая практическое задание, следует не только соблюдать принцип «от простого к сложному», но и предоставить студенту методику для самостоятельной работы дома [5].
Обнаружена взаимосвязь между эргономикой и статистическими исследованиями.
Выявлена типология дизайна эмпирических исследований с учетом особенностей объема выборки (В.В. Спасенников и соавт., 2021), ее репрезентативности и используемого математико-статистического аппарата обработки эмпирических данных [10].
Рассмотрим создание комплекта на конкретном примере.
- Постановка задачи и особенности ввода исходных данных
Рассмотрим некоторую зависимую характеристики Y, характеризующую обобщенную оценку полезности задания в зависимости от влияния некоторых (m) факторов X1, X2, … … Xm. В нашем примере учащимся предлагается выполнить 5 однотипных, но разных по формату заданий по теме «Электронные таблицы» и занести данные в рабочую таблицу – электронный реестр, рис. 1. Размещение, индексы переменных определяются удобством заполнения реестра (матрицы наблюдений, столбцы «H», «I», «J», «K», «L»), рис. 1.
Приступая к решению задачи, студент вводит код группы и фамилию в реестр; при успешном выполнении оценивает уровень сложности (X1), и комфортность (X2), работы (по 9 бальной шкале, исключая «0», субъективно). Продолжительность работы регистрируется в реестре автоматически (макрос VBA, столбец «J» (X3). Задания выполняются в любом порядке, независимо от нумерации.
Количество иллюстраций (схем, рисунков, фото) и примерный объем текстовых пояснений к заданию (X4, и X5, столбцы «K» и «L») установлены преподавателем. Ячейки для ввода данных выделены белым цветом; если реестр заполняется дистанционно (Google – таблицы), прочие ячейки следует защитить от редактирования.

Рис. 1. Фрагмент реестра выполнения заданий и регистрации времени на листе MS Excel.
Fig. 1. A fragment of the task execution and time registration registry on an MS Excel sheet.
Реестр (лист электронной таблицы) заполняет одна группа студентов. В среднем, за «пару» (90 минут) обучающиеся успевают выполнить 4 примера из 5-ти возможных, одновременно работают 10 компьютеров (учащиеся могут решать примеры вдвоем – указываются две фамилии). По окончанию эксперимента реестры всех групп объединяются вместе, строки с нулевыми полями удаляются, таблица сортируется по возрастанию номеров задания (на рис. 1. отражена начальная часть итогового реестра). По данной теме было зарегистрировано 39 верных решений (n =39): задание «01» успешно сдали 11 студентов; «02», «03», «04», «05», соответственно, 8, 8, 3, 9 обучающихся.
Фиктивная переменная x0 принимает значение «0» или «1» (пример исключен или оставлен) в результате обработки данных по алгоритму.
- Построение факторной модели комфорта (тривиальный подход).
Фактическое время выполнения заданий – важная характеристика, прямо или косвенно влияющая на комфорт и в целом отражающая нарастание сложности примера по факту.
С целью определения наилучшей пропорции между количеством иллюстраций и пояснений в комплекте определим коэффициенты уравнения bi: T = b0 + b1 x4 + b2 x5.
Точки, сгруппированные (ориентированные) вертикально, рис. 2 – одинаковые примеры, решаемые с различной скоростью. Расчет матрицы корреляций (программа «Statistica») подтверждает хаотические колебания дат (в двух плоскостях).», табл. 1, рис.2.
Зависимость времени выполнения задания от количества иллюстраций и пояснений может быть выражена уравнением линейной регрессии: T = 3,09 - 0,00 x4 + 0,40 x 5, однако коэффициенты при переменных (табл. 2) статистически незначимы. Фиктивная переменная x0 в данном случае принимает значение «1».
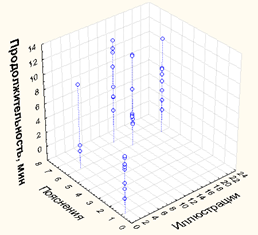
Рис. 2. Распределение дат в трехмерном пространстве.
Fig. 2. The distribution of dates in three-dimensional space.
Таблица 1.
Матрица корреляций времени выполнения примеров, числа иллюстраций и объема пояснений.
Table 1.
A matrix of correlations of the execution time of examples, the number of illustrations and the volume of explanations.
|
Переменная |
Корреляции (Spreadsheet1) Marked correlations are significant at p < ,05000 N=39 (Casewise deletion of missing data) |
||
|
Продолжительность, мин |
Иллюстрации |
Пояснения |
|
|
Продолжительность, мин |
1,00 |
0,22 |
0,29 |
|
Иллюстрации |
0,22 |
1,00 |
0,77 |
|
Пояснения |
0,29 |
0,77 |
1,00 |
Таким образом, линейный прогноз времени выполнения задания в нашем примере излишне чувствителен к набору дат и вряд ли поможет выбрать подходящий комплект примеров для учебы.
Таблица 2.
Оценка параметров линейной регрессии времени выполнения электронных примеров.
Table 2.
Estimation of the parameters of linear regression of the execution time of electronic examples.
|
N=39 |
Regression Summary for Dependent Variable: Продолжительность, мин (_Матрица__39_Набл.sta) R= ,28689595 R?= ,08230928 Adjusted R?= ,03132647 F(2,36)=1,6145 p<,21308 Std.Error of estimate: 3,3726 |
|||||
|
Бета |
Std.Err. of Beta |
B |
Std.Err. of B |
t(36) |
p-level |
|
|
ОТРЕЗОК |
|
|
3,09388 |
1,20759 |
2,56204 |
0,01474 |
|
Иллюстрации |
-0,00127 |
0,25124 |
-0,00054 |
0,10755 |
-0,00506 |
0,99599 |
|
Пояснения |
0,28788 |
0,25124 |
0,40418 |
0,35274 |
1,14584 |
0,25942 |
В случае выполнения комплекта на расстоянии прогноз показателей будет еще более размытым.
3. Алгоритм и программные средства расчета «идеализированной» выборки
Гипотеза В.А. Савицкой [8] основана на результатах повторяющихся отборов, значимую роль в которых играют эфемерные, в том числе – органолептические оценки и интуиция экспериментатора; высокопроизводительные персональные устройства для детализации пропорций «идеала», подобные современным, в тот период не существовали.
Метод применим к тем специфическим условиям, когда эффективен многократный перебор дат и повторение эксперимента во времени.
Если характеристики объектов эфемерны, реальная точность оценок снижается до уровня «1» и «0» (оставить – исключить объект). Любой отдельно взятый показатель – не «идеален», отбор наилучших дат по одному параметру (интегральной оценке Y) может изначально ввести исследователя в заблуждение. В частности, задание проще доработать и вернуть в комплект, чем строить сложные прогнозы.
В отличие от «эталона» нейронной сети, «идеал» пластичен и привязан к некоторому ограничению (по В.А. Савицкой - географическому ареалу), т.е. несет в себе внутреннюю гармонию, которая, в наиболее обобщенном представлении, связана с синхронностью колебаний переменных, т.е. ориентацией векторов Xi в пространстве (косинусное сходство).
Соответственно, «идеал» подразумевает и координаты «идеального» центра (центроида) гармонизированной выборки, отличные от совокупности.
Для любой пары приведённых величин (характеристик, параметров) xij: cos φij = cov (Xi, Xj) = rij. В нашем примере i, j = 1,2, … 5, i ≠ j, φij – угол между векторами, rij – коэффициент парной корреляции, cov (Xi, Xj) – ковариация. Функция y = |cos x| на интервале 0 ÷ 2π имеет два максимума «1» и «-1»; для наглядности перейдем трехмерному изображению.
Функция Z =∑(|rij |)/k = ∑ ( ||cos φij |)/k; принимает значения от 0 до 1, где i, j = 1,2, 3; i ≠ j; k – количество коэффициентов rij. Корреляция r23 предсказуема: количество иллюстраций и пояснений преподаватель подбирает сам, рис.1, табл.1.
Рассмотрим сумму ожидаемых значений коэффициентов, r12 и r23, k = 2, рис. 3, левый график. Локальные максимумы функции наблюдаются в 4-х точках: Zmax = (|1| + |1|)/2 = 1, далее – (|-1| + |1|)/2 = 1; (|1| + |-1|)/2 = 1 и (|-1| + |-1|)/2 = 1. Очевидно, любое значение Zij ≤ 1 принадлежит этой поверхности, рис.3.

Рис. 3. Область изменения функции Z =∑ |cosφij|/2; с ограничением для Z ≥ 0,50
Fig. 3. The area of change of the function Z =∑ |cosφij|/2; with a restriction for Z ≥ 0,50
Оптимальный набор соответствует экстремуму многомерной нелинейной функции Zmax =∑ |rij|/k = ∑ |cos φij|/k = ∑ |cov (Xi, Xj)|/k; i ≠ j для стандартизированных наблюдений; где k – количество предполагаемых значений коэффициентов rij, которые мы рассчитываем, моделируя синхронное колебание дат.
Целевая ячейка (MS Excel "Поиск решения") содержит алгоритм Z = ∑|rij | /k → max; соответственно, максимальная величина среднего значения |rij|, Z ≤ 1.
Изменяемые ячейки (фиктивные переменные (x0i, табл. 1), принимают значения "0" или "1"; в ограничениях модели указываем желаемое число заданий в комплекте: ∑|x0i| = объем гармонизированной выборки.
На первый взгляд, существует множество комбинаций с одинаковым значением Zmax.
Однако есть вычислительные тонкости, связанные с установкой ограничений для параметров «идеала»:
– исключим комплекты с нулевой вариацией xij (σxj = 0) и крайние, нетипичные даты (выбросы) ограничением варьирования σxj, интервалом 0,5 ÷ 1,5;
– ограничим отклонения выборочных средних относительно центра рассеяния (0,0±2,0/√n);
– установим ограничение по минимуму для нижней границы целевой функции Zmax, рис. 3, правый график.
С увеличением размерности пространства, как правило, одна или несколько характеристик выделяются не только по силе, но и по количеству тесных корреляций [4, 6]. Если в совокупности существуют скрытые (r ≥ 0,7) взаимосвязи, касающиеся определенных объектов, соответствующая величина угла между векторами составит: arccos (0,7071) ≈ 45° или π/4. Смена знака коэффициента корреляции подразумевает угол> π/2 и отражает дисгармонию комплекта. В итоге, расчет локализуется на наиболее «удачной» из «изолированных» вершин (рис. 3, правый график; при увеличении размерности – сочетании вершин), или «поиск» остановится на одном из вариантов семейства решений, что в принципе, информативно.
Отметим, что реальную оценку взаимосвязей (матрицу корреляций) для идеализированной выборки мы можем получить только при повторении эксперимента, т.е. уже с заданиями гармонизированного комплекта.
Метод эффективен для совокупностей со слабыми корреляциями характеристик объектов. Если матрица корреляций обнаруживает устойчивые взаимосвязи, «идеал» сводится к подтверждению существующих закономерностей.
4. Анализ состава гармонизированной выборки.
Для визуализации «идеала» удобна диаграмма, отражающая стандартизированные даты, упорядоченные по возрастанию значений одного из факторов – например, уровня сложности примера (с точки зрения студентов), рис. 4., правый график.

Рис. 4. Показатели совокупности и гармонизированной выборки: наблюдения упорядочены по сложности заданий.
Fig. 4. Indicators of the aggregate and the harmonized sample: the observations are ordered by the complexity of the tasks.
Левый график отражает данные совокупности (n = 39); правый – «идеализированной» выборки из 12 решений, в котором хаотичные колебания характеристик (m = 5), сглажены путем многочисленных итераций по вышеуказанному алгоритму.
В «идеальный» набор вошли, в порядке возрастания сложности (балл), следующие задания: «01»; «01»; «01»; «01»; «03»; «5»; «03»; «02»; «02»; «03»; «03»; «03», рис.4, правый график. Пример «4» в выборку не попал.
Возможно, задания: «01»; «02»; «03» слишком просты и малоинформативны, однако выполняя их, студенты постепенно переходят от простого к сложному, и ощущают себя более комфортно. Примеры «4» и «5» следует исключить или доработать в плане лаконичности.
Если задания выполняются в одном и том же классе, перспективно скомпоновать гармонизированный (виртуальный) комплект – по данным за семестр, постепенно дополняя набор новыми заданиями, и исключая проверенные: итоговая таблица выглядит так, словно ее заполнила в один день – одна большая группа обучающихся, рис.1. По факту, в комплект войдут наиболее «откатанные» примеры указанной темы, хотя и выполненные в разное время, разными группами. Повторные серии испытаний приблизят электронный комплекс к «идеалу» или, по крайней мере, канонизируют пропорции.
Обратные корреляции указывают на дисгармонию комплекта, и, соответственно, необходимость разработки более конструктивных, сложных решений в рамках тематики.
В нашем примере «идеал» – это некоторый пластичный, т.е. динамический электронный фильтр, с ограничениями по конкретной тематике и условиям класса, который позволяет рассчитать, не вникая в детализацию, по матрице наблюдений, путем однократного вычислительного действия – оптимизированную по плавности перехода характеристик, выборку.
Заключение
Высокопроизводительные персональные устройства, современные программы, онлайн сервис, доступные графические средства в целом поддерживают плавный переход от единичных примеров – к гармоничным комплексам, позволяющим увлечь, охватить слушателя всецело и разносторонне.
Как и произведения искусства, гармонизированные комплекты или отдельные примеры, упражнения, тренажеры – в принципе не могут быть простыми: в их создании лежит опыт проб и ошибок, долгая «ручная» работа, интуиция.
Разработку, поиск, аккумуляцию электронных заданий можно ускорить, используя средства оптимизации и осуществляя мониторинг выполнения примеров в классах.
Эмпирический «идеал» В.А. Савицкой позволяет уловить едва заметные тенденции синхронного (асинхронного) колебания оценок, характеристик учебных заданий. Нередко, именно малозаметные и слабо изученные показатели, исследуемые в массе, позволят улучшить или кардинально изменить эргономику коллективной работы в классе, наметить перспективы повышения комфорта решения сложных и углубленных задач.
Виртуальный выбор, идеализация, как приемы повышения эффективности учебного процесса могут быть рекомендованы для многих дисциплин, курсов – там, где возможности обновления, ассортимент и база примеров, тренажеров и электронных заданий к этому располагают.
1. Багрецов С.А., Шалонов Е.В., Розанова Л.В. Применение активной стратегии актуализации потенциальных свойств человеко-машинных комплексов в процессах их проектирования и эксплуатации // Эргодизайн. 2021. №3 (13). С. 188-196. DOIhttps://doi.org/10.30987/2658-4026-2021-3-188-196. EDN REOKEA.
2. Барсукова Н.И. К вопросу об универсалиях в художественно-проектной деятельности // Эргодизайн. 2021. №1 (11). С. 49-56. DOIhttps://doi.org/10.30987/2658-4026-2021-1-49-56. EDN PXDLAE.
3. Вехтер Е.В., Ефременко А.А., Радченко В.Ю. и др. Особенности визуального восприятия информационно-коммуникационных объектов // Эргодизайн. 2020. №4 (10). С. 186-193. DOIhttps://doi.org/10.30987/2658-4026-2020-4-186-193. EDN JDZDMD.
4. Денисов Д.П., Огрызков В.Е. Виртуальная селекция (virtual selection) как метод познания в образовательной среде // Проблемы современного образования. 2016. № 3. С. 107-115. EDN WFGOFR.
5. Овчинников Ю.Д. Применение метода проектных технологий с использованием эргономико-биомеханических характеристик в учебном процессе // Стандарты и мониторинг в образовании. 2022. №. 2. С. 13-19. DOIhttps://doi.org/10.12737/1998-1740-2022-10-2-13-19. EDN EIOMNZ.
6. Огрызков В.Е., Денисов Д.П., Курьяков И.А. Методика и алгоритмы диагностики ASMR и их использование в образовательном процессе // Сибирский торгово-экономический журнал. 2014. № 1(19). С. 83-88. EDN TANTPD.
7. Рытов М.Ю., Спасенников В.В. Теоретико-прикладные вопросы отбора и подготовки операторов человеко-машинных комплексов в отечественной эргономике // Эргодизайн. 2020. №4 (10). С. 203-224. DOIhttps://doi.org/10.30987/2658-4026-2020-4-203-223. EDN JDZDMD.
8. Савицкая В.А. Разработка идеала интенсивного сорта твердой пшеницы для восточных районов страны // Селекция и семеноводство. 1977. № 4. С. 8–12.
9. Сергеев С.Ф. Интеллектный техносимбиоз в сложных человеко-машинных системах // Эргодизайн. 2021. №1 (11). С. 70-76. DOIhttps://doi.org/10.30987/2658-4026-2021-1-70-76. EDN SXGDYW.
10. Спасенников В.В., Хохлова М.В., Ермакова Е.А. Когнитивная эргономика как методологическая основа педагогического дизайна // Эргодизайн. 2021. №2 (12). С. 145-150. DOIhttps://doi.org/10.30987/2658-4026-2021-2-145-150. EDN RFLCIU.
11. Moran T.P. The command language grammar: a representation for the user interface of interactive computer systems. International journal of man-machine studies. 1981;15:3-50. DOIhttps://doi.org/10.1016/S0020-7373(81)80022-3.
12. Van der Veer G.C. Cognitive Ergonomics in Interface Design - Discussion of a Moving Science. Journal of universal computer science. 2008;14:2614-2629. DOIhttps://doi.org/10.3217/jucs-014-16-2614.












