employee
Bryansk, Bryansk, Russian Federation
employee
Bryansk, Bryansk, Russian Federation
UDK 621.891 Общие вопросы. Трение в машине
The work objective is to develop methods for defining the friction coefficient of fractal surfaces. The problem to which the paper is devoted: estimation of the friction coefficient. Research methods: modelling of contact interaction, analytical calculations. The novelty of the work: the friction coefficient of fractal surfaces is estimated based on the estimation of the force interaction of microirregularities. Results of the study: the procedure for defining the components of the friction coefficient depending on the parameters of fractal roughness is presented; quantitative results of the friction coefficient of fractal surfaces are obtained. Conclusions: the fractal contact model is implemented at low contact pressure, and with the growth of the fractal dimension, the friction coefficient decreases.
fractal, fractal surfaces, external friction, models of contact interaction, friction coefficient
Введение
В более ранних работах по данной тематике исследователи полагали, что статическое трение возникает за счет механических взаимодействий шероховатых поверхностей на уровне микромасштаба [1]. Линейная зависимость силы трения от нормальной нагрузки в теории Кулона-Амонтона определялась наклоном неровностей. При этом коэффициент статического трения оказывался пропорциональным тангенсу угла наклона 
[2]. Линейное соотношение между фактической площадью контакта и нормальной силой, наблюдаемое часто в экспериментальных исследованиях, используется для оценки адекватности предлагаемой модели механики контакта. Боуден и Тейбор [3] отмечали влияние на сопротивление относительному сдвигу твердых тел молекулярного взаимодействия на физическом контакте твердых тел.
В настоящее время полагают, что трение и сопутствующие процессы, определяющие поведение пары трения, зависят не столько от свойств элементов пары, сколько от структуры всей трибологической системы, включающей промежуточную и окружающую среду, а также разного рода воздействия на систему. Это имеет особое значение в трибосистемах в условиях низкой нагрузки, где сопротивление относительному сдвигу элементов пары трения может не показать линейную зависимость от нормальных сил [4].
Следует отметить исследования по изучению зависимости фрикционных явлений от параметров шероховатости таких, как, например, арифметическое среднее отклонение ординат неровностей Ra и др. [5]. Кроме того, для оценки статического трения используют свойства материала, соотношение твердости элементов пары, распределение высот шероховатой поверхности и форму неровностей [6]. Эти исследования обычно строились на основе определённого распределения высот шероховатости с принятыми неровностями в виде сферических сегментов.
Модель контактного взаимодействия
На рис. 1. приведены поверхности, имеющие разную структуру при одной и той же амплитудной характеристике – среднеквадратичного отклонения высот.
а) б)
Рис. 1. Поверхности: а – фрактальная; б – модель Гринвуда-Вильямсона
Fig. 1. Surfaces: a - fractal; b – Greenwood-Williamson model
Инженерные поверхности имеют многоуровневые отклонения от правильной формы, присущие фрактальным объектам и характеризуемые статистическим самоподобием [7], и таким образом, в последние годы фрактальная природа привлекает все большее внимание исследователей в области анализа инженерных поверхностей и задач, связанных с контактной механикой [8, 9].
В работе [10] представлена структура и взаимодействие фрактальных поверхностей. На рис. 2а – показана модель элементарного взаимодействия неровностей фрактальных шероховатых поверхностей и на рис. 2б – их силовые взаимоотношения. Здесь ai - площадь пятна, которая предполагается равноценной с ее проекцией ввиду малого угла наклона неровностей θ.
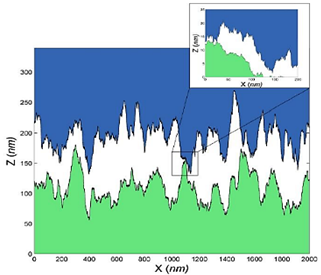
Рис. 2. Фрактальные поверхности: а – схема контакта, б – их силовые взаимодействия
Fig. 2. Fractal surfaces: a – contact diagram, b – their force interactions
1. O'Connor J., Johnson K. The role of surface asperi-ties in transmitting tangential forces between met-als. Wear. 1963; 6:118-39.
2. Müser M.H., Wenning L., Robbins M.O. Simple microscopic theory of Amonton's laws for static friction // Phys rev lett. 2001; 86:1295. DOI:https://doi.org/10.1103/PhysRevLett.86.1295.
3. Bowden F., Tabor D. The area of contact between stationary and between moving surfaces Proceed-ings of the royal society of London series A - Math-ematical and physical sciences. 1939:391-413.
4. Adams G.G., Müftü S., Azhar N.M. A scale-dependent model for multi-asperity contact and friction Journal of tribology. 2003;125:700-8.
5. Menezes P.L., Kailas S.V. Effect of surface rough-ness parameters and surface texture on friction and transfer layer formation in tin-steel tribo-system J. mater process technol. 2008;208:372-82.
6. Greenwood J., Williamson J. Contact of nominally flat surfaces Proceedings of the royal society of London series A - Mathematical and physical sci-ences. 1966;295:300-19.
7. Go J.Y., Pyun S.I. Fractal approach to rough sur-faces and interfaces in electrochemistry Modern as-pects of electrochemistry. Springer, 2006. P. 167-229.
8. Yan W., Komvopoulos K. Contact analysis of elas-tic-plastic fractal surfaces Journal of applied phys-ics. 1998; 84(7):3617.
9. Kuo X., Yuan Y., Jianjiang C. The effects of size distribution functions on contact between fractal rough surfaces AIP Advances 8. 2018;075317:1-14.
10. Hanaor D.A., Gan Y., Einav I. Static friction at fractal interfaces Tribology International. 2016; 93:229-238.
11. Mihin N.M. Vneshnee trenie tverdyh tel. M.: Nauka, 1977. 221 s.
12. Yaii W. Contact analysis of elastic-plastic fractal surfaces Journal of applied physics. 1998;84(7):3617.
13. Madzhumdar A., Bhushan B. Fraktal'naya model' uprugoplasticheskogo kontaktirovaniya sheroho-vatyh poverhnostey // Sovremennoe mashino-stroenie. Ser. B. 1991. №6. S. 11-23.
14. Zhao Y., Yang Ch., Cai L., Shi W., Hong Y. Stiff-ness and damping model of bolted joints with une-ven surface contact pressure distribution Strojniški vestnik - Journal of Mechanical Engineering. 2016;11(62):556-677.
15. Whitehouse D.J., Archard J.F. The Properties of random surfaces of significance in their contact Proceedings of the royal society of London A. 1970;316:97-121.
16. Jackson R.L., Streator J.L. A multiscale model for contact between rough surfaces. Wear. 2006;261(1112):1337-1347.
17. Jackson R.L., Green I. A statistical model of elasto-plastic asperity contact be-tween rough surfaces Tribology international. 2006;9(39):906-914.
